時角の計算と表示

時角(Hour angle)の計算

カーチス・デジカメ法などで、極軸を調整するために利用するツールです．

(1)望遠鏡や望遠レンズの焦点距離と(2)デジタルカメラのCCDなど撮像素子のサイズ、(3)北極星の真の北極からのオフセット、以上の３個のパラメータと観測日時、観測場所の経度のから、極軸（デジカメの視野の中心）が真の北極を向いたときに北極星がカメラの画面上に表示される位置を計算します．

これは、北極星の「時角(hour angle)」と呼ばれています．

極軸を合わせるには、赤道儀のマウントを調整し、時角に対応した位置へ北極星を導入します．

続いて、極軸を中心に赤道儀を回転させ、北極星がこのツールを利用して表示した極軸パターンの円周上を移動することを確認します．

もし、北極星が円周上から外れる場合は、赤道儀のマウントの微調整を繰り返します．

時角は、観測日時、観測地の経度から次の順序で一意に計算することが可能です．

計算の手順

（１）観測日時からユリウス日を計算する．

（２）ユリウス日からグリニッジ恒星時を計算する．

（３）グリニッジ恒星時と観測地の経度から地方恒星時を計算する．

（４）地方恒星時と北極星の赤経から、時角を計算する．

インターネットで調べると、いろいろな計算式があって、計算結果に多少の違いがあるようですが、とりあえずここでは無視することにします ;-)

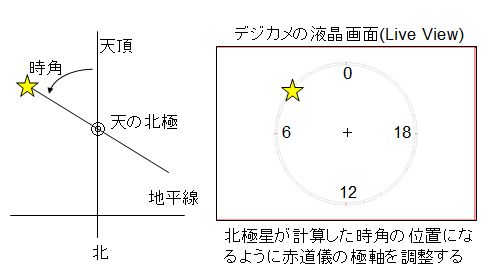
北極星の位置は、倒立像の場合と正立像の場合で異なります．

観測日時 2025/01/08 09:53 JST

観測地の緯度 139.75°　　(139°45′)

準ユリウス日 60683.45

グリニッジ恒星時 08:04:21

地方恒星時 17:23:21

時角 14:37:22

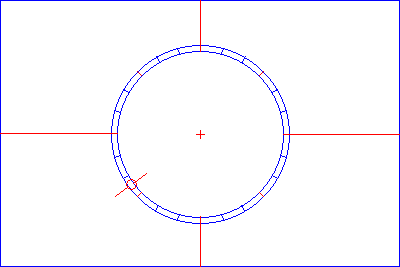
正立像（DPPA法や直接焦点撮影による見え方）

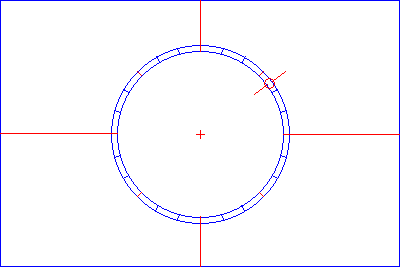
倒立像(極軸望遠鏡での見え方）

計算式

ユリウス日の計算

function proc_MJD($y,$m,$d,$h,$mi){
/*
 $y 年, $m 月, $d 日, $h 時, $mi 分
*/
  if($m<=2) {
        $y=$y-1;
        $m=$m+12;
  }
  $ret=(int)(365.25*$y)+ (int)($y/400) - (int)($y/100);
  $ret+= (int)(30.59*($m-2)) + $d - 678912;
  $ret+= $h/24 + $mi/1440 - 0.375;
  return $ret;
}

地方恒星時の計算

function proc_LST($mjd,$la){
/*  
 $mjd ユリウス日,   $la 観測地の経度
*/
  $d=0.671262 + 1.0027379094 * ( $mjd - 40000) + $la/360;
  $ret=24*($d - (int)($d));
  return $ret;
}

参考になるLINK

EQASCOM EQ6 Pro,SE2赤道儀などをASCOM対応にするドライバ

TAKAHASHIの極望（？）をイメージしたパターンへ計算した時角を表示するオンライン・ツール(http://www.takahashi-europe.com/support/softwares/polarisfinder/polarisfinder-1.5-en.htm)

観測日時	2025/01/08 09:53 JST
観測地の緯度	139.75°　　(139°45′)
準ユリウス日	60683.45
グリニッジ恒星時	08:04:21
地方恒星時	17:23:21
時角	14:37:22